Null

Du befindest dich hier:

Die 0 ist keine Zahl ?

...das sagen die Mathematiker... wie auch immer, die Null ist ein wichtiger Bestandteil unserer Ziffern.
Würde es sie nicht geben könnten wir Zahlen wie zum Beispiel 10, 20, 30, 40 usw. gar nicht ausdrücken.
Es sieht ganz so aus, als ob die Null notwendigerweise auftauchen musste, damit unser Zahlensystem überhaupt funktionieren kann.
Gut für uns also, dass die 0 in Indien er- oder gefunden wurde...
Aber nicht nur die Null wurde entdeckt - etymologisch ist die Null mit dem Wort Ziffer (für Zahlzeichen) verbunden, das auf das arabische Wort "sifr" zurückgeht.
Es lässt sich beispielsweise durch den Begriff "erzählen" die deutliche Verbindung von Zahlen und Worten erkennen. Die Ziffer führt uns über das Wort "entziffern" zur
Decodierung bzw. Entschlüsselung von Chiffrierungen (Kodierungen). Interessant auch der Begriff Luziffer und die alte Meinung dass die Ziffer Null (auch Leere, Nichts) magische Kräfte besitze

Die Null und die Acht:
Diese beiden haben eine einzigartige Eigenschaft, die sie von allen anderen Ziffern abhebt: Ihre Linienführung ist unendlich. Man könnte sagen, dass die 8 aus 2 Nullen besteht. Eine querliegende 8 -> oo symbolisiert die Unendlichkeit.

Die Null, der Kreis und die Quadratur des Kreises:
Die 0 ist eine Art Kreis. Der Kreis gilt eigentlich als Unendlicheck.
Die so genannte Quadratur des Kreises gilt als unmöglich.
In Holofeeling lese ich aber, dass es doch möglich ist und zwar einfacher als mancher denken mag. Vielleicht sind es nur kleine Denkfehler, die uns den Wald vor lauter Bäumen nicht sehen lassen:

Hier erst mal eine

Falschaussage: "Einen Kreis zu quadrieren bedeutet seinen Umfang in 4 gleichgroße Teile zu zerlegen um dann aus den 4 Teilen ein Quadrat mit gleichem Umfang zu bilden."
...dies ist verkehrt! Der Umfang muss nicht gleich sein, sondern die Fläche - und das gleichflächige Quadrat muss nur mit Zirkel und Lineal aus dem Kreis konstruiert werden !
Wichtig : Wenn man aus einer gleichen Strecke/Umfang (z.B. einem Faden) verschiedene Figuren formt (Kreis, Viereck, Dreieck usw.) hat zwar jede Figur den gleichen Umfang aber eine andere Fläche.

Wir bleiben noch etwas beim Kreisumfang...
Die Aussage: Man nimmt zum Beispiel einen Faden, bildet daraus einen Kreis (z.B. Faden um einen Flasche legen). Man teilt den Faden in 4 gleichgroße Teile und bildet so daraus ein Quadrat mit gleichem Umfang.
...ist fast richtig denn: man könnte so ein Quadrat mit dem annähernd gleichen Kreis-Umfang bilden - Wichtig: die Quadratfläche ist nicht gleich der Kreisfläche !
Hier die Formel für die Berechnung des Kreisumfanges: U = d x p.
p (Pi = 3,1415926535897932....unendlich) ist ein irrationaler Wert.
Es ist also weder rechnerisch noch konstruktiv möglich auf vier 100%ig exakt gleichlange Quadrat-Seitenlängen zu kommen. Praktisch ist das aber egal, weil diese geringen Ungenauigkeiten zum Beispiel bei baulichen Anwendungen nicht ins Gewicht fallen.
Genauso verhält es sich auch bei der Berechnung der Kreisfläche: A = p x r² .
Bevor ich aber zur Quadratur komme noch folgende Frage zum Umfang von Flächen:
Wie errechnet sich die maximale und wie die minimale Fläche zu einem vorgegebenen Umfang "X" (Welche Figurenart hat die größtmögliche und welche die kleinstmögliche Fläche ?

DIE ANTWORT:
Der Kreis (A = p x r²) hat im Vergleich die größte Fläche... bei einem vorgegebenen Umfang von zum Beispiel 6,2832...
ergibt sich eine Kreisfläche von 3,14159... (ca. p ...entspricht 100%).
Das Quadrat (A = a x a oder a²) mit dem gleichen Umfang kommt auf eine Fläche von ca. 2,467... (entspricht ca. 78,54% /-21,47%)...
und das gleichschenklige Dreieck (A = a²/4 Ö 3 ) mit dem gleichen Umfang hat nur noch ca. 1,899... (entspricht ca. 60,46% /-18,08%)
Das bedeutet also, je mehr Ecken eine Figur hat desto größer ist im Vergleich ihre Fläche.
Der Kreis als Unendlicheck betrachtet schein die Figur zu sein, die die größtmöglich erfassbare Fläche besitzt und das Dreieck ist offenbar die Figur mit dem kleinsten Fläscheninhalt.

Ist die Quadratur des Kreises doch möglich ? Ist das Alles nur ein Ansichtsproblem ?
Wie war es möglich, dass ein altes Volk wie die Ägypter ein so beeindruckendes Bauwerk wie die Cheopspyramide erbauen konnte ? (gab es die Ägypter überhaupt ?)
Man sagt, dass die Ägypter es sogar geschafft haben, die angeblich unmögliche Quadratur des Kreises in diesem Bauwerk für uns verschlüsselt zu hinterlegen...

Die Quadratur des Kreises

Die Fläche des Kreises errechnet sich auch aus dem irrationalen Wert: p x Radius ²
Das Ergebnis kann darum immer nur eine An-Näherung sein.
( zur offiziellen Erklärung der Quadratur des Kreises siehe auch den unteren Link)

Im echten Leben sind die kleinen Ungenauigkeiten weniger interessant (z.B. Häuserbau). Ein Dachgiebel wird auch halten wenn das eine Stück Holz 0,1cm länger ist als das andere.
Die Architekten können bei der Konstruktion von Gebäuden die kleinen Ungenauigkeiten ignorieren.
Sie rechnen mit 3 p - Nachkommastellen. Keiner würde auf die Idee kommen mehr Stellen als nötig in die Berechnungen aufzunehmen.

In der theorethischen Mathematik sieht es offenbar so aus, als ob man aus einem Kreis kein gleichflächiges Quadrat bilden kann.
Aber was wäre wenn es doch eine Lösung gibt ? Da die Fläche eines Kreises durch die transzendente und irrationale Zahl p errechnet wird kann die Fläche nur einen transzendenten, irrationalen Wert haben.
transzendent: lat., die Grenzen der möglichen Erfahrung, des sinnlichen Wahrnehmbaren überschreitend...
irrational: nicht als ein Verhältnis zweier ganzer Zahlen darstellbar. Ihre dezimale Erweiterung geht „ewig“ weiter, ohne dass sich die letzte Stelle[n] irgendwann ständig wiederholt....

Arithmetische Quadratur des Kreises

Wie mache ich aus einem Kreis ein gleichflächiges Quadrat ?
Am Beispiel eines Kreises mit Radius = 1 ergibt sich folgender Flächenwert:
A = 1² · p ~ 3,141592654...
Ein flächengleiches Quadrat hätte also den theoretischen Flächenwert 3,141592654... ( p )
...die Seitenlänge des entsprechenden fiktiven Quadrates hätte somit den Wert:
a = 1 · p^0,5 ~ 1,772453851...
Daraus ergibt sich die allgemeine Formel zur Errechnung der Quadrat Seitenlänge: a = r · p^0,5

Wie mache ich aus dem Quadrat einen gleichflächigen Kreis ?
Am Beispiel eines Quadrates mit der Seitenlänge 1 ergibt sich umgekehrt folgender Flächenwert:
A = 1² = 1
Ein flächengleicher Kreis hätte also den theoretischen Flächenwert 1 - der Radius des entsprechenden fiktiven Kreises hätte somit den Wert:
r = 1 · p^-0,5 ~ 0,564189583...
Daraus ergibt sich die allgemeine Formel zur Errechnung des Kreis Radius: r = a · p^-0,5
! p^0,5 entspricht Öp ( also 1,772453851...) und p^-0,5 entspricht Ö(1/p) ( also 0,5641895835477562869480...) !

Dass der Wert für p = 3,141.... zwar unendlich viele Nachkommastellen hat, aber trotzdem nie die 3,15 erreicht ist ein Phänomen, dass uns öfter begegnet. Etwas ist unendlich innerhalb eines eingrenzbaren Bereiches. Ich könnte also sagen die unendlichen Pi-Nachkommastellen liegen zwischen 3,14 und 3,15 - In einem wirklich kleinen Bereich von ca. 0,01 läuft der unendliche Zahlenstrang von p
Ich könnte aber auch sagen der Bereich liegt zwischen 3,141 und 3,142 - dann wären er nur noch 0,001 groß.
Das gleiche passiert auch wenn ich einen Kreis um etwas ziehe. Auf der Linie des Kreises oder der Null kann ich mich unendlich lange in eine Richtung bewegen. Der Bereich den die Linie umzieht wird allerdings durch sie abgegrenzt.
Die Undenlichkeit in der Endlichkeit - eine Frage der Betrachtungsweise.

...mehr zu Pi:

Die Null und die Sonne Als ich die Ordnung unserer 9 Planeten betrachtete fiel mir auf, dass sie von der Sonne aus abgezählt werden. Das bedeutet : wenn nach der Sonne der Merkur der 1. Planet, die Venus der 2., die Erde der 3. Planet usw. ist, dann kann man der Sonne eigentlich die 0 zuordnen.

Das tat ich auch... in einem tabellarischen Zahlensystem ordnete ich in horizontaler aufsteigender Reihenfolge jedem Planeten seine Zahl zu und der Sonne die 0. Danach lies ich einen Zahlenstrahl, wiederum mit 1 beginnend von der 0 aus gesehen fortlaufend und vertikal nach unten laufen. Nun teilte ich die vertikalen Zahlen durch alle horizontalen:
1:1, 1:2, 1:3 ...usw.
2:1, 2:2, 2:3 ...usw.
3:1, 3:2, 3:3 ...usw.
Bald hatte ich ein Koordinatensystem voll mit Werten die auf den ersten Blick ungeordnet erschienen aber bei genauerem Hinsehen erkannte ich ein System.
Erst sah ich, dass die 1 in diagonaler Richtung nach unten in regelmäßigen Abständen bei den Teilungs-Ergebnissen war. Dann aber sah ich, dass dies für alle Zahlen zutrifft. Ich verband alle gleichen Zahlen mit einer Linie und siehe da - Die Linien führten strahlenförmig auf einen einzigen Punkt -
Und dieser Punkt war die 0 -die Sonne-
Nachdem ich das Koordinatensystem erweitert und weitere Linien verbunden hatte zeigte sich eine "strahlende Sonne" bzw. 1/4 Ausschnitt von Ihr.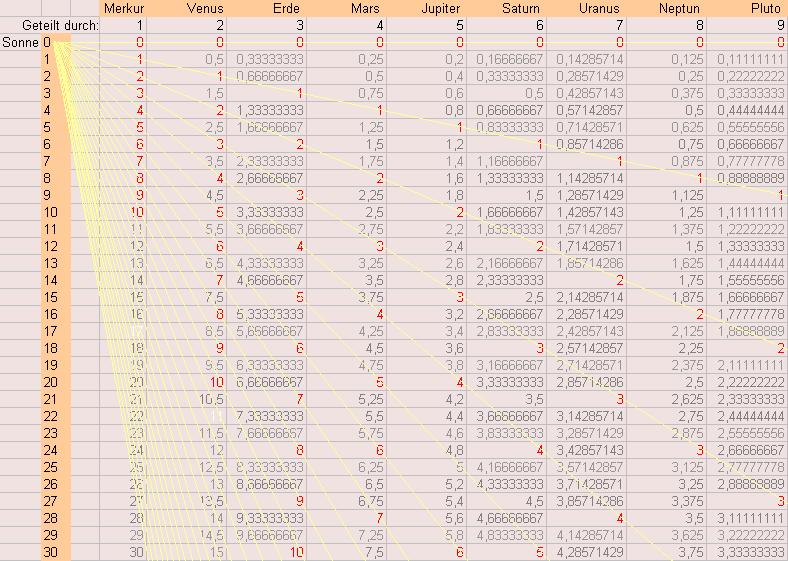

Du befindest dich hier: Geschichte - Zahlen - Null